03.12 D+2

요소 곱셈, 행렬 곱셈, 내적에 관하여

• 요소 곱셈
  • Broadcasting을 통해 서로 다른 크기의 배열끼리도 곱셈이 가능하다.
  • 사용: *
• 행렬 곱셈 (matrix multiply)
  
  • 행렬 간의 전체적인 곱셈 연산이다.
  • 사용: @, matmul()
• 행렬 내적
  • 두 행렬 간의 각 성분별 곱셈 후 합산을 의미한다.
  • 사용: np.dot()

1) 행렬 곱셈과 요소 곱셈의 차이 예시

import torch

A = torch.tensor([[1, 2], [3, 4]])
B = torch.tensor([[5, 6], [7, 8]])

# 행렬 곱셈
C = A @ B
print(C)
# 출력: tensor([[19, 22],
#               [43, 50]])

# 요소별 곱셈
D = A * B
print(D)
# 출력: tensor([[ 5, 12],
#               [21, 32]])

2) 행렬 곱셈과 행렬 내적: 공통점 및 차이점

• 공통점:아래의 경우에는 결과가 같게 나온다.
  1. 1차원 * 1차원 (내적 연산)
  2. 2차원 * 2차원 (2차원 행렬곱)
  3. 2차원 * 1차원 or 1차원 * 2차원 (행렬 * 벡터곱 연산)
  
• 차이점:
  1. 배열과 스칼라 곱: 내적은 지원하지만, 행렬곱셈은 오류가 난다.
  2. 3차원 이상 다차원 배열: 행렬곱셈은 외적 역할을 한다.

참고:

- https://seong6496.tistory.com/110

- https://jimmy-ai.tistory.com/104

- https://blogik.netlify.app/BoostCamp/U_stage/04_AI_math/

 

Reshaping

- view도 사용할 수 있다.

 

Pytorch를 쓰는 이유

- vectorized operations인 텐서를 사용하면 병렬처리하여 더 빠르게 계산할 수 있기 때문이다.

 

Backpropagation할 때 변수들의 size 비교하기

• X.shape: torch.Size([20, 3])
• Y.shape: torch.Size([20, 2])
• W1.shape: torch.Size([3, 4])
• B1.shape: torch.Size([1, 4])
• W2.shape: torch.Size([4, 2])
• B2.shape: torch.Size([1, 2])

def backprop(x):
    # TODO: forward pass
    z1 = x @ W1 + B1
    h = torch.relu(z1)
    z2 = h @ W2 + B2
    y_hat = torch.sigmoid(z2)

    # TODO: backward pass
    y_hat_grad = 2 * (y_hat - Y)
    z2_grad = y_hat_grad * y_hat * (1 - y_hat)
    h_grad = z2_grad @ W2.T
    z1_grad = h_grad * (z1 >= 0).float()

    # calculate parameter gradients
    B2_grad = z2_grad.sum(0)
    W2_grad = (h[:,:,None] * z2_grad[:,None,:]).sum(0)
    B1_grad = z1_grad.sum(0)
    W1_grad = (X[:,:,None] * z1_grad[:,None,:]).sum(0)

    # output tuple of gradients for all parameters
    return W1_grad, B1_grad, W2_grad, B2_grae

연산 후 변수들의 모양:

• z1 (첫 번째 레이어의 가중치 합): X와 W1의 행렬곱의 결과이므로 모양은 torch.Size([20, 4])
• h (ReLU 적용 후): z1과 동일한 모양인 torch.Size([20, 4])
• z2 (두 번째 레이어의 가중치 합): h와 W2의 행렬곱의 결과이므로 모양은 torch.Size([20, 2])
• y_hat (시그모이드 적용 후): z2와 동일한 모양인 torch.Size([20, 2])

그래디언트의 모양:

• y_hat_grad: y_hat과 동일한 모양인 torch.Size([20, 2])
• z2_grad: y_hat_grad와 같은 연산을 거쳐도 모양은 변하지 않으므로 torch.Size([20, 2])
• h_grad: z2_grad @ W2.T의 연산 결과이므로 모양은 torch.Size([20, 4])
• z1_grad: h_grad에 ReLU의 미분을 적용한 결과이므로 모양은 torch.Size([20, 4])

파라미터 그래디언트의 모양:

• B2_grad: z2_grad.sum(0)의 결과로, 모양은 torch.Size([2]).sum(0)은 배치에 대해 합산하는 연산이므로, 결과는 B2의 모양과 동일
• W2_grad: h.T @ z2_grad의 결과로, 모양은 torch.Size([4, 2])h.T는 h의 전치이며, 이 연산의 결과는 W2의 모양과 일치.
• B1_grad: z1_grad.sum(0)의 결과로, 모양은 torch.Size([4]). 이는 B1의 모양과 동일합니다 (편향은 일반적으로 차원을 1개 감소시키며 합산).
• W1_grad: X.T @ z1_grad의 결과로, 모양은 torch.Size([3, 4]). 이는 W1의 모양과 일치

 

위 backpropagation에서 요소 곱셈과 행렬 곱셈의 차이

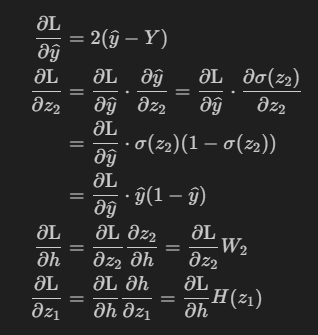
위의 그림에서 '·'  기호가 있고 없을 때가 있다. 보통 '·' 기호는 내적을 의미하지만, 이걸 혼동해서 쓰는 사람도 있어서 두 가지 방식의 곱셈 중 어느 것이 의도되었는지는 주변 맥락이나 해당 분야의 규칙에 따라 결정된다.

• 행렬 곱셈: 행렬과 벡터(또는 행렬과 행렬)이 수식에서 연속해서 나타나고, 인덱스가 명시적으로 언급되지 않으면 행렬 곱셈이 의도되었다고 볼 수 있다. e.g) W와 h 사이의 연산.
• 요소 곱셈: 같은 크기의 두 벡터 또는 요소가 연속해서 나타나면, 요소 곱셈이 의도되었다고 볼 수 있다. e.g) 벡터 v와 그 미분 dv/dx의 곱

 

 

'요소별 곱셈과 행렬 곱셈을 적용하는 이유는 각 연산이 수행하는 작업의 차이이다.

 

Autograd

Pytorch에서 Autograd는 backward()를 호출하면 자동으로 백워딩 된다.

# x is just an example tensor
# `requires_grad_` tells PyTorch to store gradients for the tensor
x = torch.tensor([2., 3., 4.]).requires_grad_(True)

# `x.grad` is currently empty, because we haven't called `backward()` on anything
print(x.grad) # None

# Notice that this is the same calculation, but the gradients increase!
# This shows that `.backward()` adds to the gradients without resetting them
y = (x**2 + x).sum()
print(y) # tensor(38., grad_fn=<SumBackward0>)
y.backward()
print(x.grad) # tensor([20., 28., 36.])

근데 x.grad는 업데이트할때마다 계산된 gradients들이 누적된다. 따라서 매 training iteration마다 zero_grad()를 써야한다.그렇지 않으면, training iteration할 동안 gradients는 계속 쌓이게 된다.

 

optimizer.zero_grad(), loss.backward(), optimizer.step()

• optimizer.zero_grad() : 이전 step에서 각 layer 별로 계산된 gradient 값을 모두 0으로 초기화 시킨다. 0으로 초기화 하지 않으면 gradient가 누적합으로 계산된다.
• loss.backward() : 각 layer의 파라미터에 대해 back-propagation을 통해 gradient를 계산한다.
• optimizer.step() : 각 layer의 파라미터와 같이 저장된 gradient 값을 이용하여 파라미터를 업데이트한다. (weight가 업데이트 되는 시점이다)
• 순서: loss 계산 -> backward로 gradient 계산 -> optimizer.step()으로 weight 업데이트

 

nn.Module

class Model(nn.Module):  # replace "Model" with what you want to call the network class
    def __init__(self):  # constructor defined as `__init__`. You can also provide args.
        super().__init__()  # call the super class's constructor for PyTorch to properly register it as an `nn.Module`
        # store the model's parameters in fields
        self.conv1 = nn.Conv2d(1, 20, 5)  # nn.Conv2d is one of PyTorch's many built-in layers
        self.conv2 = nn.Conv2d(20, 20, 5)

    def forward(self, x):  # the `forward` method is how you run the model, and `__call__` gets aliased to it
        # this is where you should implement the forward pass
        x = self.conv1(x).relu()
        return self.conv2(x).relu()

 

language model의 다음 단어 예측 방법

language model은 다음 단어에 대한 확률 분포를 예측한다.

좋은 LM은 현재 맥락에서 말이 되는 next-token에 더 높은 확률을 부여하는 모델이다.

1) 디코딩 방법1: greedy decoding

• 각 스텝마다 most likely next-token을 예측한다.
• 단점: input이 같으면 다양한 output을 내기 어렵다.

2) 디코딩 방법2: Sampling

• most-likely token을 생성하는 것보다, 예측된 확률분포로부터 샘플링
• 단점: 다양한 결과를 만들 수 있지만, 말이 안되는 경우도 있다.

이외에도 여러 디코딩 방법이 있다. optimal decoding 전략은 generation 목표에 따라 다르다. (e.g. accuracy, creativity)