섹션 8: 동적 계획법 (Dynamic programming)
Bottom-Up적 다이나믹 프로그래밍
한번에 문제를 해결하기 어렵다.
작은 단위의 문제 크기로 바꾼다. 바꾼 문제를 해결. 답을 따로 저장. (1)
조금 큰 단위의 문제 크기로 접근. 만약 *2하면 해결된다는 것을 발견. (2)
조금 더 확장한 문제 크기로 접근. *2를 한다면 해결되는 것을 발견 (4)
점화식: f(n) = 2 x f(n-1)
→ 작은 해를 직관적으로 구할 수 있게 한뒤, 앞의 해를 이용해서 그 다음 해를 구하기
일차원 배열에다 반복문이 돌면서 하기
(동적계획법 방식)
Top-Down적 다이나믹 프로그래밍
위와 비슷한 식으로 하지만, 재귀를 쓴다.
불필요한 반복을 줄이기위해 구한 값은 배열 or 리스트에 저장한다. (메모이제이션)
메모이제이션이 있어야 다이나믹 프로그래밍이다. 없으면 그냥 재귀.
(넓은 의미의 동적 계획법 방식)
1번: 네트워크 선 자르기 (Bottom-Up)

2번: 네트워크 선 자르기 (Top-Down)
7m가 주어지면: (6m로 자른 경우의 수 + 1m) + (5m로 자른 경우의 수 + 2m)
dy에 해당 값 저장한다. 왜냐하면 D(4)의 경우 2번 구해야되어서 저장안하고 재귀로만 하면 비효율이라.

3번: 도전과제
만약 특정 돌다리를 디딜수 없다고 하면 0으로 넣기.
4번: 최대 부분 증가수열 (LIS)
5 3 7 8 7 2 9 4 가 있을 때,
예를 들어 8이다.
8을 마지막 항으로 하는 증가수열은
3 7 8
5 7 8
3 8
5 8
로 4가지이다.
dy: 해당 값을 마지막 항으로 했을 때, 여러 경우들 중 가장 긴 수열의 길이

마지막 항을 답으로 출력하는 것이 아니라 dy의 최대값을 출력한다.
5번: 최대 선 연결하기 (LIS 응용)
최대 증가수열과 비슷한 문제.
왼쪽은 나열되어있으니 오른쪽에서 점차 증가된거 고르면 된다.
※ 응용: 다 연결하고 최소 몇개의 선을 제거해야 교차하지 않는 선을 제일 많이 남길 수 있는지도 물어본다.
6번: 가장 높은 탑 쌓기 (LIS 응용)
밑면의 넓이 순으로 정렬 후, 무게 조건 만족하기.
dy[2]: 2번 블록이 제일 꼭대기에 있을 때 탑의 최대 높이.
7번: 알리바바와 40인의 도둑 (Bottom-Up)
2차원 리스트 배열인 dy에 만들기.
dy[i][j]: i, j까지 가는데 최소 비용.
8번: 알리바바와 40인의 도둑 (Top-Down)
D(2, 2)의 return 값: 2, 2에 도달하는데 드는 최소 에너지 비용.
메모이제이션이니깐 기록하기.

9번: 가방문제 (냅색 알고리즘)
dy[j]: 가방에 j라는 무게까지 가방에 담을 수 있을 때, 보석의 최대 가치.

10번: 동전교환 (냅색 알고리즘)
dy[j]: j원을 거슬러주는데 사용된 동전의 최소 개수
dy[j - coin[i]] + 1: j원을 거슬러주는데 coin[i]을 하나 씀. 그래서 +1 한다.
coins[i]가 2이고 j가 2일 때: dy[2 - 2] + 1 = dy[0] + 1 = 1이 된다. -> 2원은 2동전 하나.
6일때: 5원짜리 하나 + 1원짜리일 때 최소.
11번: 최대점수 구하기 (냅색 알고리즘)
한 유형당 한개만 풀 수 있다. -> 그래서 2차원 테이블로 하기
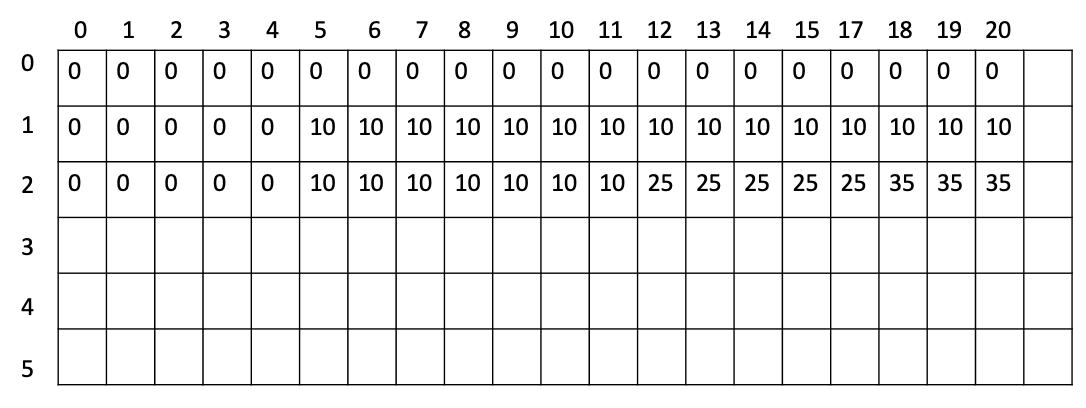
dy[i][j]: i번째까지 문제를 적용. j 제한시간.
pt: 적용되는 문제의 제한시간
pv: 적용되는 문제 가치
dy[i-1]번째까지 적용한 것 참조. 그 행의 [j-pt]참조.
2번째 행 적용하기 전에 미리 윗행 복사해서 2번째 행에 붙이기.
그런데 실제에서는 이렇게 2차원하지 않는다. 왜냐하면 공간복잡도가 너무 커서. -> 그래서 실전에서는 1차원으로 해결한다.

dy[j]: j라는 분이 나한테 주어졌을 때 얻을 수 있는 최대 점수.
앞에서부터하면 중복적용이 되니 뒤에서부터 한다.
pv=10, pt=5일 때: 20분이 주어지면 20-5=15. dy[15]에는 0이 있어서 10이 들어간다.
12번: 플로이드-와샬 (그래프 최단거리)

dis[i][j] = i정점에서 j정점으로 가는 최소 비용 값.
k를 거치는 for문 만들기. -> 3중 for 문
13번: 회장뽑기 (플로이드-와샬 응용)
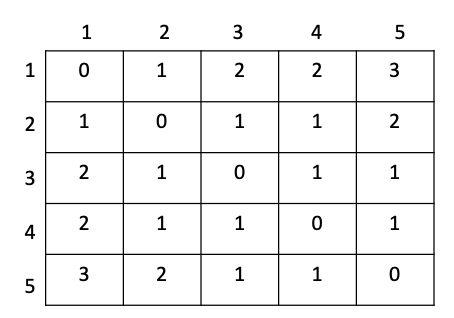
입력정보를 그래프로 표현.
res 리스트에 각 사람별 최댓값 기록.
14번: 위상정렬 (그래프)
위상정렬: 일의 선후관계를 유지하면서 전체 일의 순서를 짜는 알고리즘.
차수: 연결된 간선의 개수
진입차수: 들어오는 차수

degree라는 1차원 테이블에 진입차수 만들기
큐에 차수가 0인 것 넣기. (1, 6)
1이 나오면 1이 만드는 진입차수 없애기 -> 4번이 2에서 1로 감소.
6이 나오면 6이 만드는 진입차수 없애기 -> 2번이 0으로 감소. -> 큐에 넣기.