섹션6: 완전탐색 (백트랙킹, 상태트리와 CUT EDGE)-DFS(깊이우선탐색)기초

재귀함수가 작동될 때 스택을 사용한다.

재귀함수: 반복문의 효과를 낼 수 있다.

def DFS1(x):
	if x> 0:
		DFS(x-1)
        print(x, end='')
        
def DFS2(x):
	if x> 0:
    	print(x, end='')
		DFS(x-1)

DFS1(3) # 1 2 3 출력됨 
DFS2(3) # 3 2 1 출력됨

 

1번: 재귀함수를 이용한 이진수 출력

return만 쓰면 함수 종료

 

2번: 이진트리 순회 (DFS: Depth First Search)

트리 순회 방법: 1. 깊이 우선 탐색(DFS), 2. 너비 우선 탐색(BFS) <- 나중에

- 전위 순회: 본인 것을 출력하고 왼쪽자식, 오른쪽 자식을 방문. (대표적)

   부모 -> 왼쪽 자식 -> 오른쪽 자식

   1 2 4 5 3 6 7

- 중위 순회:

   왼쪽 자식 -> 부모 -> 오른쪽 자식

   4 2 5 1 6 3 7

- 후위 순회: (병합 정렬 문제 대표)

   왼쪽 자식 -> 오른쪽 자식 -> 부모

   4 5 2 6 7 3 1

 

3번: 부분집합 구하기

부분집합은 특정 원소가 들어가는지 안 들어가는지로 2가지 경우의 수가 있다.

{1, 2, 3}의 부분집합의 경우의 수는 2x2x2 - 1(공집합) = 7이다.

여기서 착안하여,

 

4번: 합이 같은 부분집합

위와 같은 방식으로 트리 형성.

전체 원소의 합을 total이라고 구한 뒤, total - 트리로 구한 부분집합의 합 = 다른 부분집합의 합

 

p.s) 시간 복잡도 단축하는 방법:

sum > total//2일 경우 함수를 종료한다. 

sum == (total//2)로 하면 안된다. 왜냐하면 6과 7인데 13//2 = 6으로 해서 잘못 될 수도 있어서.

 

5번: 바둑이 승차 - Cut Edge Tech

트럭에 태울 수 있는 경우: 부분집합

현재 트럭에 태운다/태우지 않는다를 부분집합에 적용하였다.

 

시간 복잡도 줄이는 방법!

태운다고 판단을 한 합에 누적

앞으로 적용할 바둑이들의 무게: total - tsum(지금까지 판단한 무게 합 누적)

밑가지들 다 더해도 result보다 작으면 진행할 필요가 없다.

 

6번: 중복순열 구하기

 

7번: 동전 교환 - Cut Edge Tech

 

8번: 순열 구하기

 

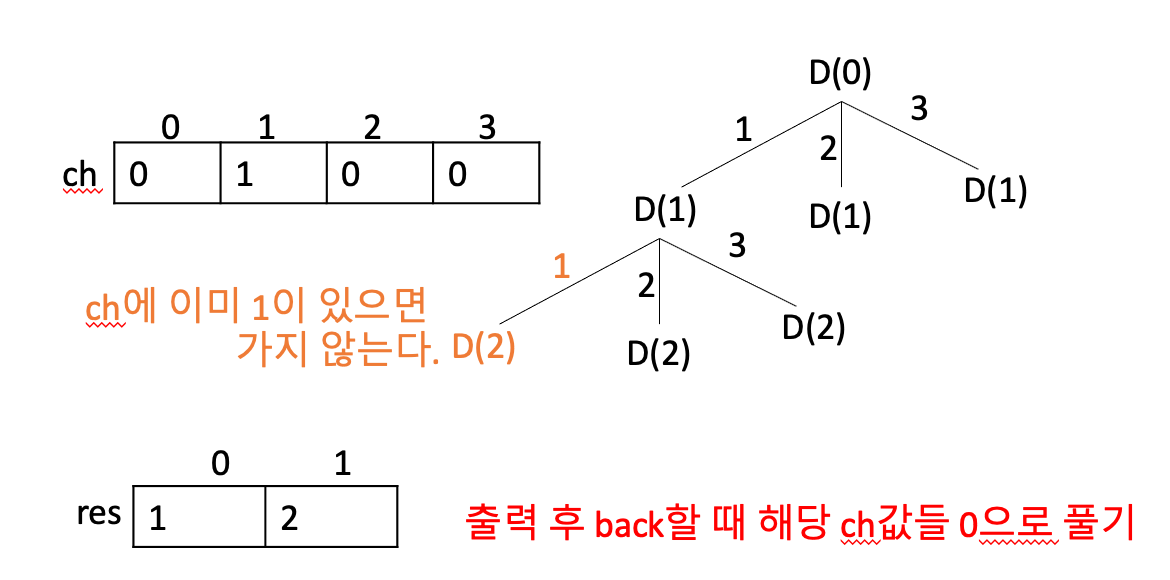
9번: 수열 추측하기(순열, 파스칼 응용)

 

10번: 조합구하기

 

11번: 수들의 조합

 

12번: 라이브러리를 이용한 순열

import itertools as it

it.permutations

*의존하지 말자!

 

13번: 라이브러리를 이용한 조합

import itertools as it

it.combinations

*의존하지 말자!

 

14번: 인접행렬 (가중치 방향그래프)

노드와 간선.

그래프: 노드와 간선의 집합.

방향이 설정되어 있으면 방향 그래프.

+ 간선에 값이 있으면: 가중치 방향 그래프

 

15번: 경로 탐색 (DFS: 깊이 우선 탐색)